← return to practice.dsc40a.com
Instructor(s): Aobo Li
This exam was administered in person. Students had 50 minutes to take this exam.
Source: Winter 2024 Midterm 2, Problem 1
Quarks are one of the smallest fundamental particles in physics. There are 6 types of quarks: up, down, top, bottom, strange, charm. Each one of the 6 types of quarks can be in two states: quark or antiquark.
Consider an experiment where we select n quarks uniformly at random. The result of the experiment is a description of the type and state of the quark selected. For example, if n=3, one possible result is:
Selected quark 1 is a top quark.
Selected quark 2 is a charm antiquark.
Selected quark 3 is a top antiquark.
How many results are possible for this experiment with n quarks?
6^n
9^n
12^n
18^n
36^n
None of the above.
12^n
Each quark has 6 \cdot 2 = 12 possibilities because there are 6 possible types and 2 possible states. Since our experiment involves independently picking one of these 12 possibilities for each of our n quarks, the total number of results for the experiment is 12^n.
A meson is formed by combining two quarks. In order to form a meson, the two quarks must satisfy the following rules:
They must be in different states: one must be a quark and the other one must be an anti-quark.
The two quarks can be the same type: i.e. top quark and top antiquark can form a meson.
The order of quark and antiquark does matter.
Consider an experiment where we select n mesons uniformly at random. How many results are possible for this experiment?
2^n
6^n
12^n
18^n
36^n
None of the above.
None of the above (72^n).
For making a meson, we need to choose two quarks. The first quark we choose has 6 \cdot 2 = 12 possibilities because there are 6 possible types and 2 possible states. However, our second quark cannot have the same state as our first; so the second quark has 6 \cdot 1 = 6 possibilities because there are still 6 possible types, but only 1 possible state.
This means a single meson has 12 \cdot 6 = 72 possibilities. (If the order of the quark and antiquark did not matter, it would instead have \frac{72}{2} = 36 possibilities). So, an experiment where we select n mesons uniformly at random has 72^n unique results.
Source: Winter 2024 Midterm 2, Problem 2
A special poker card deck contains the 52 standard cards:
| Heart: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A |
| Diamond: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A |
| Club: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A |
| Spade: 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A |
…plus two wildcards: a Red Joker and a Black Joker. The total number of cards in this card deck is 54.
How many different four-card hands can be selected from this deck? (Note: order does not matter in a card hand.)
{54 \choose 4} = 316251
Since order does not matter, we would use a combination instead of a permutation here. From 54 unique cards in our poker deck, we can choose 4 at random to get a card hand.
An alternative way to think about it: there are 54 options for the first card we pick, 53 for the second card, 52 for the third card, etc. For four cards, we have 54 \cdot 53 \cdot 52 \cdot 51 hands. However this will count the same hand in different card orders as different hands, which we don’t want. To correct this, we divide by 4! (4 \cdot 3 \cdot 2 \cdot 1), because each unique hand will appear 24 times but in different orders.
\frac{54 \cdot 53 \cdot 52 \cdot 51}{4 \cdot 3 \cdot 2 \cdot 1} = {54 \choose 4} = 316251
For this deck, how many 5 card hands are there that include four-of-a-kind (four cards of the same value)? Show your work.
650
Since the first 4 cards are four-of-a-kind (same number), there are 13 ways to select a four-of-a-kind. For the 5th card, there are 50 total choices (12 remaining values \cdot 4 suits + 2 wildcards). So there are a total 13 \cdot 50 = 650 options.
In certain poker rules, a bomb is defined as either four-of-a-kind, or two wildcards (red joker and black joker). Suppose you randomly draw a 4 card hand and you found a bomb in it, what is the probability that the bomb is four-of-a-kind? Show your work.
P(\text{Four of a kind | Bomb}) = \frac{1}{103}
The number of hands containing two jokers (the other two cards are arbitrary) is given by: \begin{align*} \underbrace{{2 \choose 2}}_{\text{Two Jokers}} \cdot \underbrace{{52 \choose 2}}_{\text{Other Two Cards}} = \frac{52 \cdot 51}{2} = 1326. \end{align*} The number of hands that form four of a kind is 13, one for each of the 13 unique values in a deck.
For a bomb to occur, the four cards either contain two jokers or form four of a kind. Hence, \begin{align*} P(\text{Four of a kind | Bomb}) = \frac{13}{13 + 1326} = \frac{1}{103} \end{align*}
Source: Winter 2024 Midterm 2, Problem 3
Schrödinger’s cat is a famous thought experiment in quantum mechanics proposed by physicist Erwin Schrödinger in 1935. The experiment is described below:
“Imagine there’s a hypothetical cat in a closed box with a toxic radioactive element that might decay. If it decays, the cat dies; if it doesn’t, the cat lives.”
Please note that Schrödinger’s Cat is a purely theoretical concept, so a thought experiment. It has never been executed in the real world, and no cats have ever been harmed as a result of it.
Suppose the cat has 90 \% of the chance to die if the decay happens. The cat also has 10 \% chance to die even if the decay does not happen. Suppose the decay happens with a 20 \% probability. After you open the box, you find the cat dead. What is the probability that the decay happened?
P(\text{Decay|Dead}) = \frac{18}{26}
The probability we are looking for is P(\text{Decay|Dead}). Using Bayes’ theorem, we can write:
\begin{align*} P(\text{Decay|Dead}) = \frac{P(\text{Dead|Decay})P(\text{Decay})}{P(\text{Dead})} \end{align*}
Using the Law of Total Probability, we can rewrite the denominator:
\begin{align*} P(\text{Decay|Dead}) = \frac{P(\text{Dead|Decay})P(\text{Decay})}{P(\text{Dead|Decay})P(\text{Decay}) + P(\text{Dead|Not Decay})P(\text{Not Decay})} \end{align*}
We know that:
\begin{align*} P(\text{Dead|Decay}) &= 90\% = 0.9\\ P(\text{Dead|Not Decay}) &= 10\% = 0.1\\ P(\text{Decay}) &= 20\% = 0.2 \end{align*}
Plugging these numbers, we have:
\begin{align*} P(\text{Decay|Dead}) &= \frac{0.9\cdot 0.2}{0.9 \cdot 0.2 + 0.1 \cdot (1-0.2)}\\ &=\frac{18}{26} \end{align*}
Quantum superposition is a mind-bending and counter-intuitive concept in physics. In the Schrödinger’s cat scenario, when the box is closed, the cat can be both dead and alive simultaneously. However, once we open the box and observe, the superposition collapses, and the cat must be either dead or alive, not both.
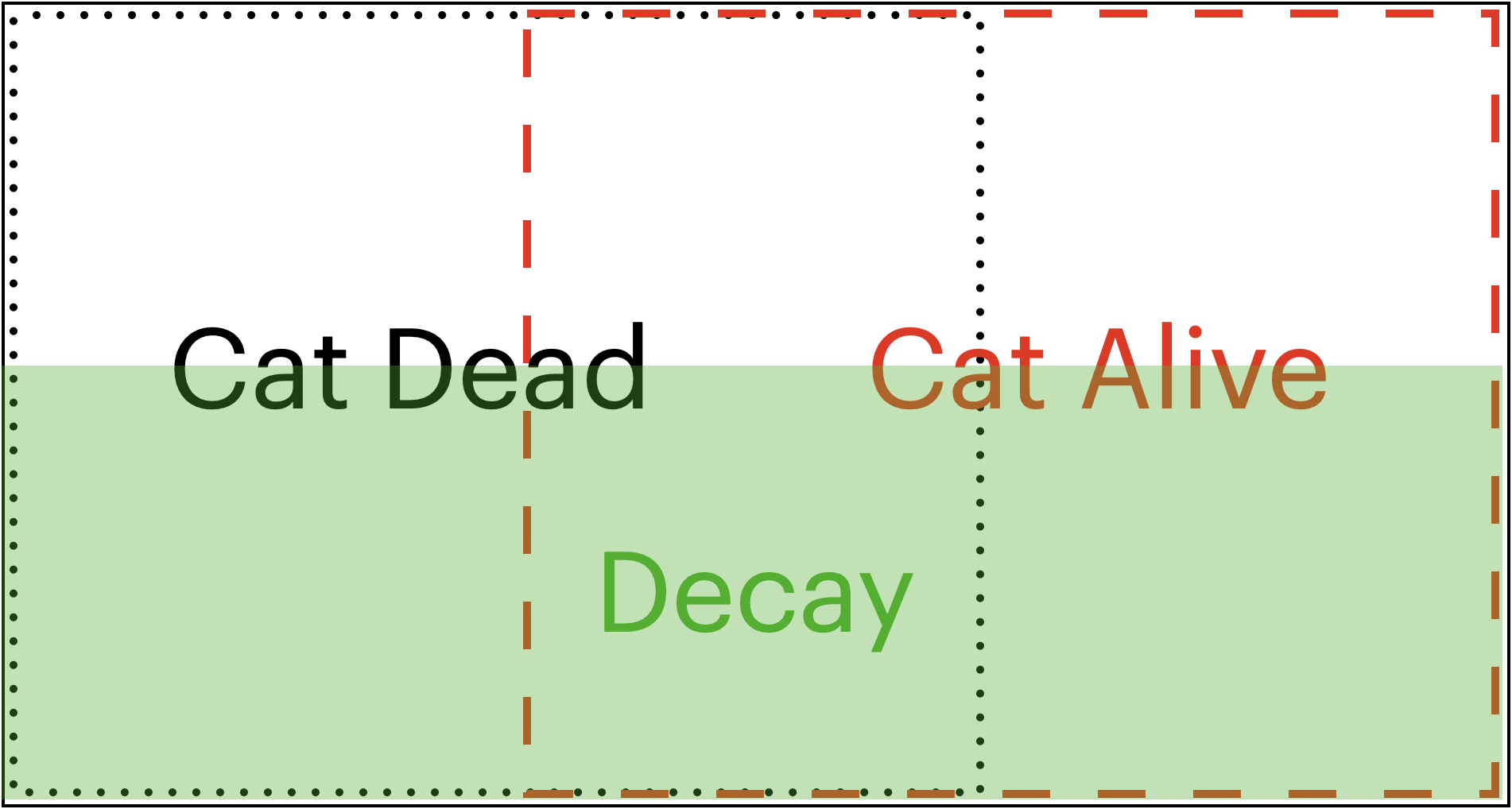
The Venn Diagram below depicts the Schrödinger’s cat scenario with the box closed. In this diagram, the black dotted line is the event of cat dead, the red dashed line denotes the event of cat being alive, and the shaded region is the event of decay.

Based on this Venn diagram, which of the following is true? Select all that apply:
Decay is independent of Cat Dead
Decay is independent of Cat Alive
Cat Dead and Cat Alive are mutually exclusive.
Cat Dead, Cat Alive, and Decay form a partition of the sample
None of Above.
Statements 1 and 2 are true. Statements 3, 4, and 5 are false.
When two events are independent, the following statement is true: P(\text{Event 1}) = P(\text{Event 1} | \text{Event 2}). So for statement 1, we need to show: P(\text{Decay}) = P(\text{Decay} | \text{Cat Dead})
These two fractions look the same. So that means the independence equation holds, and statement 1 is true.
We can do the same thing but instead with the “Cat Alive” region to also show that statement 2 is true.
The “Cat Alive” and “Cat Dead” regions intersect, implying those two events can occur at the same time. If two events can occur at the same time, they are not mutually exclusive, so statement 3 is false.
A partition of a sample is a perfect division the sample space into a bunch of little pieces, without any overlaps or empty space. For this problem, it would mean finding a way to perfectly divide the Venn Diagram. You cannot divide the Venn Diagram into the regions “Cat Dead”, “Cat Alive”, and “Decay”; go ahead and try, no matter how you slice it the overlaps will mess up the division. This means that “Cat Dead”, “Cat Alive”, and “Decay” do not form a partition of the sample, so statement 4 is false.
Since statements 1 and 2 were true, the answer cannot be none of the above, so statement 5 is false.
You’re given the following probabilities:
P(\text{Cat Dead} \cup \text{Decay}) = \dfrac{4}{5}
P(\text{Cat Alive} \cup \text{Decay}) = \dfrac{1}{2}
P(\text{Cat Alive} \cup \text{Cat Dead}) = 1
P(\text{Decay}) = \dfrac{1}{5}
Using the Venn diagram in Problem 3.2, calculate the probability for Schrodinger’s cat to be in the superposition state (i.e. both dead and alive):
P(\text{Alive} \cap \text{Dead}) = \frac{1}{8}
Since we know that the decay is independent to cat’s state, we have: \begin{align*} P(\text{Dead} \cup \text{Decay}) &= P(\text{Dead}) + P(\text{Decay}) - P(\text{Dead} \cap \text{Decay})\\ &=P(\text{Dead}) + P(\text{Decay}) - P(\text{Dead})\cdot P(\text{Decay}) = \frac{4}{5} \end{align*}
Similarly, we have: \begin{align*} P(\text{Alive} \cup \text{Decay}) &= P(\text{Alive}) + P(\text{Decay}) - P(\text{Alive} \cap \text{Decay})\\ &=P(\text{Alive}) + P(\text{Decay}) - P(\text{Alive})\cdot P(\text{Decay}) = \frac{1}{2} \end{align*}
We are given P(\text{Decay}) = \frac{1}{5}, so we can plug it into the equations we made for P(\text{Dead} \cup \text{Decay}) and P(\text{Alive} \cup \text{Decay}): \begin{align*} &P(\text{Dead} \cup \text{Decay}) = P(\text{Dead}) + \frac{1}{5} - (\frac{1}{5} \cdot P(\text{Dead})) = \frac{4}{5}\\ \\ &P(\text{Alive} \cup \text{Decay}) = P(\text{Alive}) + \frac{1}{5} - (\frac{1}{5} \cdot P(\text{Alive})) = \frac{1}{2}\\ \\ \end{align*}
Solving these two equations, we have: \begin{align*} &\frac{4}{5} = P(\text{Dead}) + \frac{1}{5} - (\frac{1}{5} \cdot P(\text{Dead})) \\ &(\frac{4}{5}) \cdot 5 = (P(\text{Dead}) + \frac{1}{5} - (\frac{1}{5} \cdot P(\text{Dead}))) \cdot 5 \\ &4 = 5 \cdot (P(\text{Dead})) + 1 - P(\text{Dead}) \\ &3 = 4 \cdot (P(\text{Dead})) \\ &P(\text{Dead}) = \frac{3}{4} \end{align*} and \begin{align*} &\frac{4}{5} = P(\text{Alive}) + \frac{1}{5} - (\frac{1}{5} \cdot P(\text{Alive})) \\ &(\frac{1}{2}) \cdot 10 = (P(\text{Alive}) + \frac{1}{5} - (\frac{1}{5} \cdot P(\text{Alive}))) \cdot 10 \\ &5 = 10 \cdot (P(\text{Alive})) + 2 - 2 \cdot P(\text{Alive}) \\ &3 = 8 \cdot (P(\text{Alive})) \\ &P(\text{Alive}) = \frac{3}{8} \end{align*}
The probability of a superposition state is P(\text{Alive} \cap \text{Dead}). Since we know that P(\text{Alive} \cup \text{Dead}) = 1 we have:
\begin{align*} P(\text{Alive} \cup \text{Dead}) &= P(\text{Alive}) + P(\text{Dead}) - P(\text{Alive} \cap \text{Dead})\\ \end{align*}
Rearranging terms, we have: \begin{align*} P(\text{Alive} \cap \text{Dead}) &= P(\text{Alive}) + P(\text{Dead}) - P(\text{Alive} \cup \text{Dead})\\ &= \frac{3}{4} + \frac{3}{8} - 1\\ \\ &= \frac{6}{8} + \frac{3}{8} - 1\\ \\ &=\frac{1}{8} \end{align*}