← return to practice.dsc40a.com
Instructor(s): Suraj Rampure
This exam was administered in person. Students had 180 minutes to take this exam.
Source: Spring 2024 Final, Problem 1
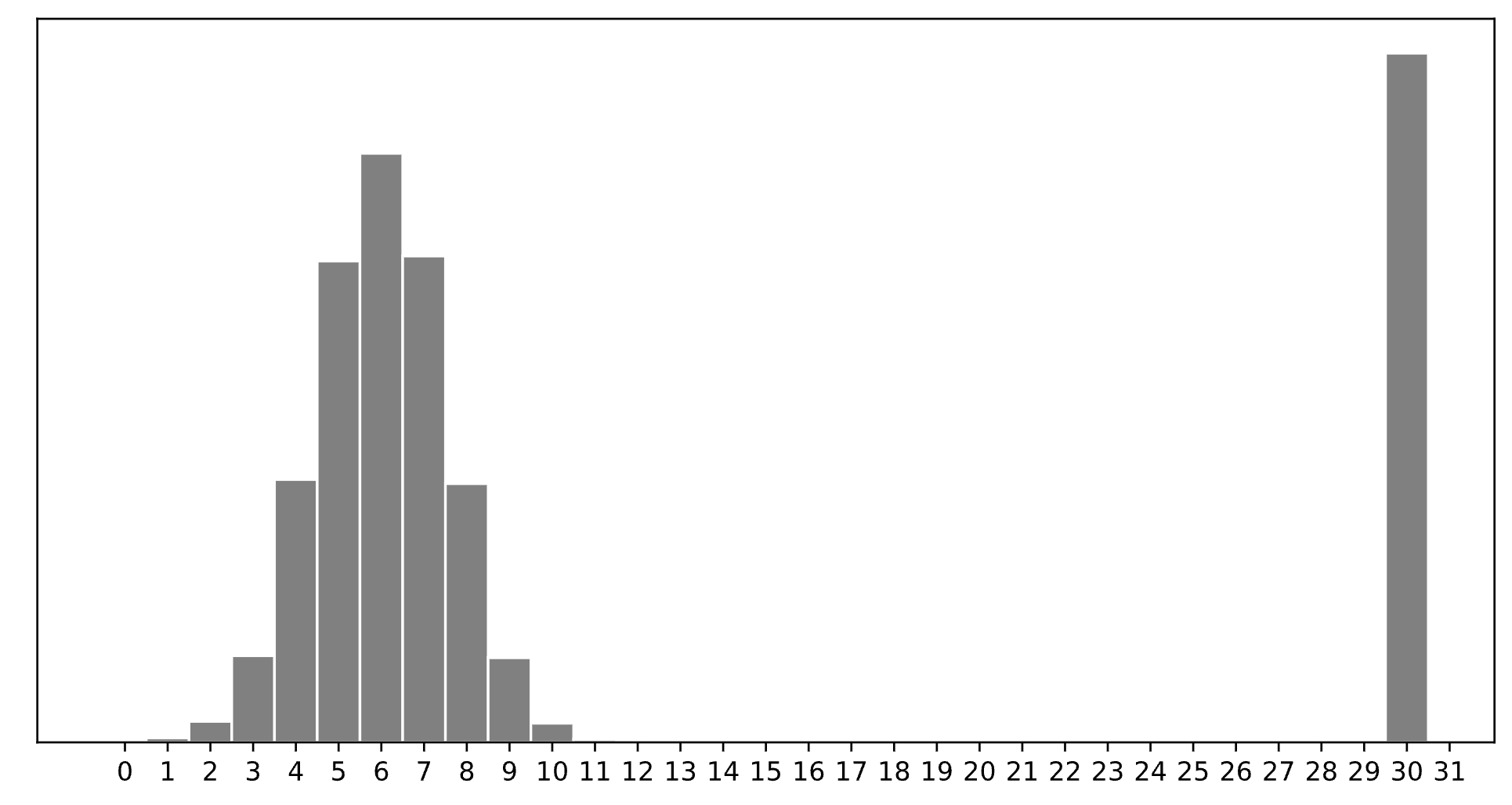
Consider a dataset of n integers, y_1, y_2, ..., y_n, whose histogram is given below:

Which of the following is closest to the constant prediction h^* that minimizes:
\displaystyle \frac{1}{n} \sum_{i = 1}^n \begin{cases} 0 & y_i = h \\ 1 & y_i \neq h \end{cases}
1
5
6
7
11
15
30
30.
The minimizer of empirical risk for the constant model when using zero-one loss is the mode.
Which of the following is closest to the constant prediction h^* that minimizes: \displaystyle \frac{1}{n} \sum_{i = 1}^n |y_i - h|
1
5
6
7
11
15
30
7.
The minimizer of empirical risk for the constant model when using absolute loss is the median. If the bar at 30 wasn’t there, the median would be 6, but the existence of that bar drags the “halfway” point up slightly, to 7.
Which of the following is closest to the constant prediction h^* that minimizes: \displaystyle \frac{1}{n} \sum_{i = 1}^n (y_i - h)^2
1
5
6
7
11
15
30
11.
The minimizer of empirical risk for the constant model when using squared loss is the mean. The mean is heavily influenced by the presence of outliers, of which there are many at 30, dragging the mean up to 11. While you can’t calculate the mean here, given the large right tail, this question can be answered by understanding that the mean must be larger than the median, which is 7, and 11 is the next biggest option.
Which of the following is closest to the constant prediction h^* that minimizes: \displaystyle \lim_{p \rightarrow \infty} \frac{1}{n} \sum_{i = 1}^n |y_i - h|^p
1
5
6
7
11
15
30
15.
The minimizer of empirical risk for the constant model when using infinity loss is the midrange, i.e. halfway between the min and max.
Source: Spring 2024 Final, Problem 2
Consider a dataset of 3 values, y_1 < y_2 < y_3, with a mean of 2. Let Y_\text{abs}(h) = \frac{1}{3} \sum_{i = 1}^3 |y_i - h| represent the mean absolute error of a constant prediction h on this dataset of 3 values.
Similarly, consider another dataset of 5 values, z_1 < z_2 < z_3 < z_4 < z_5, with a mean of 12. Let Z_\text{abs}(h) = \frac{1}{5} \sum_{i = 1}^5 |z_i - h| represent the mean absolute error of a constant prediction h on this dataset of 5 values.
Suppose that y_3 < z_1, and that T_\text{abs}(h) represents the mean absolute error of a constant prediction h on the combined dataset of 8 values, y_1, ..., y_3, z_1, ..., z_5.
Fill in the blanks:
“{ i } minimizes Y_\text{abs}(h), { ii } minimizes Z_\text{abs}(h), and { iii } minimizes T_\text{abs}(h).”
y_1
any value between y_1 and y_2 (inclusive)
y_2
y_3
z_1
z_1
z_2
any value between z_2 and z_3 (inclusive)
any value between z_2 and z_4 (inclusive)
z_3
y_2
y_3
any value between y_3 and z_1 (inclusive)
any value between z_1 and z_2 (inclusive)
any value between z_2 and z_3 (inclusive)
The values of the three blanks are: y_2, z_3, and any value between z_1 and z_2 (inclusive).
For the first blank, we know the median of the y-dataset minimizes mean absolute error of a constant prediction on the y-dataset. Since y_1 < y_2 < y_3, y_2 is the unique minimizer.
For the second blank, we can also use the fact that the median of the z-dataset minimizes mean absolute error of a constant prediction on the z-dataset. Since z_1 < z_2 < z_3 < z_4 < z_5, z_3 is the unique minimizer.
For the third blank, we know that when there are an odd number of data points in a dataset, any values between the middle two (inclusive) minimize mean absolute error. Here, the middle two in the full dataset of 8 are z_1 and z_2.
For any h, it is true that:
T_\text{abs}(h) = \alpha Y_\text{abs}(h) + \beta Z_\text{abs}(h)
for some constants \alpha and \beta. What are the values of \alpha and \beta? Give your answers as integers or simplified fractions with no variables.
\alpha = \frac{3}{8}, \beta = \frac{5}{8}.
To find \alpha and \beta, we need to construct a similar-looking equation to the one above. We can start by looking at our equation for T_\text{abs}(h):
T_\text{abs}(h) = \frac{1}{8} \sum_{i = 1}^8 |t_i - h|
Now, we can split the sum on the right hand side into two sums, one for our y data points and one for our z data points:
T_\text{abs}(h) = \frac{1}{8} \left(\sum_{i = 1}^3 |y_i - h| + \sum_{i = 1}^5 |z_i - h|\right)
Each of these two mini sums can be represented in terms of Y_\text{abs}(h) and Z_\text{abs}(h):
T_\text{abs}(h) = \frac{1}{8} \left(3 \cdot Y_\text{abs}(h) + 5 \cdot Z_\text{abs}(h)\right) T_\text{abs}(h) = \frac38 \cdot Y_\text{abs}(h) + \frac58 \cdot Z_\text{abs}(h)
By looking at this final equation we’ve built, it is clear that \alpha = \frac{3}{8} and \beta = \frac{5}{8}.
Show that Y_\text{abs}(z_1) = z_1 - 2.
Hint: Use the fact that you know the mean of y_1, y_2, y_3.
We can start by plugging z_1 into Y_\text{abs}(h):
Y_\text{abs}(z_1) = \frac{1}{3} \left( | z - y_1 | + | z - y_2 | + |z - y_3| \right)
Since z_1 > y_3 > y_2 > y_1, all of the absolute values can be dropped and we can write:
Y_\text{abs}(z_1) = \frac{1}{3} \left( (z_1 - y_1) + (z_1 - y_2) + (z_3 - y_3) \right)
This can be simplified to:
Y_\text{abs}(h) = \frac{1}{3} \left( 3z_1 - (y_1 + y_2 + y_3) \right) = \frac{1}{3} \left( 3z_1 - 3 \cdot \bar{y}\right) = z_1 - \bar{y} = z_1 - 2.
Suppose the mean absolute deviation from the median in the full dataset of 8 values is 6. What is the value of z_1?
Hint: You’ll need to use the results from earlier parts of this question.
2
3
5
6
7
9
11
3.
We are given that T_\text{abs}(\text{median}) = 6. This means that any value (inclusive) between z_1 and z_2 minimize T_\text{abs}(h), with the output being always being 6. So, T_\text{abs}(z_1) = 6. Let’s see what happens when we plug this into T_\text{abs}(h) = \frac{3}{8} Y_\text{abs}(h) + \frac{5}{8} Z_\text{abs}(h) from earlier:
T_\text{abs}(z_1) = \frac{3}{8} Y_\text{abs}(z_1) + \frac{5}{8} Z_\text{abs}(z_1) (6) = \frac{3}{8} Y_\text{abs}(z_1) + \frac{5}{8} Z_\text{abs}(z_1)
If we could write Y_\text{abs}(z_1) and Z_\text{abs}(z_1) in terms of z_1, we could solve for z_1 and our work would be done, so let’s do that. Y_\text{abs}(z_1) = z_1 - 2 from earlier. Z_\text{abs}(z_1) simplifies as follows (knowing that \bar{z} = 12):
Z_\text{abs}(z_1) = \frac{1}{5} \sum_{i = 1}^5 |z_i - z_1| Z_\text{abs}(z_1) = \frac{1}{5} \left(|z_1 - z_1| + |z_2 - z_1| + |z_3 - z_1| + |z_4 - z_1| + |z_5 - z_1|\right) Z_\text{abs}(z_1) = \frac{1}{5} \left(0 + (z_2 + z_3 + z_4 + z_5) - 4z_1\right) Z_\text{abs}(z_1) = \frac{1}{5} \left((z_2 + z_3 + z_4 + z_5) - 4z_1 + (z_1 - z_1)\right) Z_\text{abs}(z_1) = \frac{1}{5} \left((z_1 + z_2 + z_3 + z_4 + z_5) - 5z_1\right) Z_\text{abs}(z_1) = \bar{z} - z_1 Z_\text{abs}(z_1) = (12) - z_1
Subbing back into our main equation:
(6) = \frac{3}{8} Y_\text{abs}(z_1) + \frac{5}{8} Z_\text{abs}(z_1) 6 = \frac{3}{8}(z_1 - 2) + \frac{5}{8}(12 - z_1) z_1 = 3
Source: Spring 2024 Final, Problem 3
Suppose we’re given a dataset of n points, (x_1, y_1), (x_2, y_2), ..., (x_n, y_n), where \bar{x} is the mean of x_1, x_2, ..., x_n and \bar{y} is the mean of y_1, y_2, ..., y_n.
Using this dataset, we create a transformed dataset of n points, (x_1', y_1'), (x_2', y_2'), ..., (x_n', y_n'), where:
x_i' = 4x_i - 3 \qquad y_i' = y_i + 24
That is, the transformed dataset is of the form (4x_1 - 3, y_1 + 24), ..., (4x_n - 3, y_n + 24).
We decide to fit a simple linear hypothesis function H(x') = w_0 + w_1x' on the transformed dataset using squared loss. We find that w_0^* = 7 and w_1^* = 2, so H^*(x') = 7 + 2x'.
Suppose we were to fit a simple linear hypothesis function through the original dataset, (x_1, y_1), (x_2, y_2), ..., (x_n, y_n), again using squared loss. What would the optimal slope be?
2
4
6
8
11
12
24
8.
Relative to the dataset with x', the dataset with x has an x-variable that’s “compressed” by a factor of 4, so the slope increases by a factor of 4 to 2 \cdot 4 = 8.
Concretely, this can be shown by looking at the formula 2 = r\frac{SD(y')}{SD(x')}, recognizing that SD(y') = SD(y) since the y values have the same spread in both datasets, and that SD(x') = 4 SD(x).
Recall, the hypothesis function H^* was fit on the transformed dataset,
(x_1', y_1'), (x_2', y_2'), ..., (x_n', y_n'). H^* happens to pass through the point (\bar{x}, \bar{y}). What is the value of \bar{x}? Give your answer as an integer with no variables.
5.
The key idea is that the regression line always passes through (\text{mean } x, \text{mean } y) in the dataset we used to fit it. So, we know that: 2 \bar{x'} + 7 = \bar{y'}. This first equation can be rewritten as: 2 \cdot (4\bar{x} - 3) + 7 = \bar{y} + 24.
We’re also told this line passes through (\bar{x}, \bar{y}), which means that it’s also true that: 2 \bar{x} + 7 = \bar{y}.
Now we have a system of two equations:
\begin{cases} 2 \cdot (4\bar{x} - 3) + 7 = \bar{y} + 24 \\ 2 \bar{x} + 7 = \bar{y} \end{cases}
\dots and solving our system of two equations gives: \bar{x} = 5.
Source: Spring 2024 Final, Problem 4
Consider the vectors \vec{u} and \vec{v}, defined below.
\vec{u} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \qquad \vec{v} = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix}
We define X \in \mathbb{R}^{3 \times 2} to be the matrix whose first column is \vec u and whose second column is \vec v.
In this part only, let \vec{y} = \begin{bmatrix} -1 \\ k \\ 252 \end{bmatrix}.
Find a scalar k such that \vec{y} is in \text{span}(\vec u, \vec v). Give your answer as a constant with no variables.
252.
Vectors in \text{span}(\vec u, \vec v) must have an equal 2nd and 3rd component, and the third component is 252, so the second must be as well.
Show that: (X^TX)^{-1}X^T = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{2} & \frac{1}{2} \end{bmatrix}
Hint: If A = \begin{bmatrix} a_1 & 0 \\ 0 & a_2 \end{bmatrix}, then A^{-1} = \begin{bmatrix} \frac{1}{a_1} & 0 \\ 0 & \frac{1}{a_2} \end{bmatrix}.
We can construct the following series of matrices to get (X^TX)^{-1}X^T.
In parts (c) and (d) only, let \vec{y} = \begin{bmatrix} 4 \\ 2 \\ 8 \end{bmatrix}.
Find scalars a and b such that a \vec u + b \vec v is the vector in \text{span}(\vec u, \vec v) that is as close to \vec{y} as possible. Give your answers as constants with no variables.
a = 4, b = 5.
The result from the part (b) implies that when using the normal equations to find coefficients for \vec u and \vec v – which we know from lecture produce an error vector whose length is minimized – the coefficient on \vec u must be y_1 and the coefficient on \vec v must be \frac{y_2 + y_3}{2}. This can be shown by taking the result from part (b), \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{2} & \frac{1}{2} \end{bmatrix}, and multiplying it by the vector \vec y = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \end{bmatrix}.
Here, y_1 = 4, so a = 4. We also know y_2 = 2 and y_3 = 8, so b = \frac{2+8}{2} = 5.
Let \vec{e} = \vec{y} - (a \vec u + b \vec v), where a and b are the values you found in part (c).
What is \lVert \vec{e} \rVert?
0
3 \sqrt{2}
4 \sqrt{2}
6
6 \sqrt{2}
2\sqrt{21}
3 \sqrt{2}.
The correct value of a \vec u + b \vec v = \begin{bmatrix} 4 \\ 5 \\ 5\end{bmatrix}. Then, \vec{e} = \begin{bmatrix} 4 \\ 2 \\ 8 \end{bmatrix} - \begin{bmatrix} 4 \\ 5 \\ 5 \end{bmatrix} = \begin{bmatrix} 0 \\ -3 \\ 3 \end{bmatrix}, which has a length of \sqrt{0^2 + (-3)^2 + 3^2} = 3\sqrt{2}.
Is it true that, for any vector \vec{y} \in \mathbb{R}^3, we can find scalars c and d such that the sum of the entries in the vector \vec{y} - (c \vec u + d \vec v) is 0?
Yes, because \vec{u} and \vec{v} are linearly independent.
Yes, because \vec{u} and \vec{v} are orthogonal.
Yes, but for a reason that isn’t listed here.
No, because \vec{y} is not necessarily in
No, because neither \vec{u} nor \vec{v} is equal to the vector
No, but for a reason that isn’t listed here.
Yes, but for a reason that isn’t listed here.
Here’s the full reason: 1. We can use the normal equations to find c and d, no matter what \vec{y} is. 2. The error vector \vec e that results from using the normal equations is such that \vec e is orthogonal to the span of the columns of X. 3. The columns of X are just \vec u and \vec v. So, \vec e is orthogonal to any linear combination of \vec u and \vec v. 4. One of the many linear combinations of \vec u and \vec v is \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}. 5. This means that the vector \vec e is orthogonal to \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}, which means that \vec{1}^T \vec{e} = 0 \implies \sum_{i = 1}^3 e_i = 0.
Suppose that Q \in \mathbb{R}^{100 \times 12}, \vec{s} \in \mathbb{R}^{100}, and \vec{f} \in \mathbb{R}^{12}. What are the dimensions of the following product?
\vec{s}^T Q \vec{f}
scalar
12 \times 1 vector
100 \times 1 vector
100 \times 12 matrix
12 \times 12 matrix
12 \times 100 matrix
undefined
Correct: Scalar.
The inner dimensions of 100 and 12 cancel, and so \vec{s}^T Q \vec{f} is of shape 1 x 1.
Source: Spring 2024 Final, Problem 5
Let \vec{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}. Consider the function g(\vec{x}) = (x_1 - 3)^2 + (x_1^2 - x_2)^2.
Find \nabla g(\vec{x}), the gradient of g(\vec{x}), and use it to show that \nabla g\left( \begin{bmatrix} -1 \\ 1 \end{bmatrix} \right) = \begin{bmatrix} -8 \\ 0 \end{bmatrix}.
\nabla g(\vec{x}) = \begin{bmatrix} 2x_1 -6 + 4x_1(4x_1^2 - x_2) \\ -2(x_1^2 - x_2) \end{bmatrix}
We can find \nabla g(\vec{x}) by finding the partial derivatives of g(\vec{x}):
\frac{\partial g}{\partial x_1} = 2(x_1 - 3) + 2(x_1^2 - x_2)(2 x_1) \frac{\partial g}{\partial x_2} = 2(x_1^2 - x_2)(-1) \nabla g(\vec{x}) = \begin{bmatrix} 2(x_1 - 3) + 2(x_1^2 - x_2)(2 x_1) \\ 2(x_1^2 - x_2)(-1) \end{bmatrix} \nabla g\left(\begin{bmatrix} - 1 \\ 1 \end{bmatrix}\right) = \begin{bmatrix} 2(-1 - 4) + 2((-1)^2 - 1)(2(-1)) \\ 2((-1)^2 - 1) \end{bmatrix} = \begin{bmatrix} -8 \\ 0 \end{bmatrix}.
We’d like to find the vector \vec{x}^* that minimizes g(\vec{x}) using gradient descent. Perform one iteration of gradient descent by hand, using the initial guess \vec{x}^{(0)} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} and the learning rate \alpha = \frac{1}{2}. In other words, what is \vec{x}^{(1)}?
\vec x^{(1)} = \begin{bmatrix} 3 \\ 1 \end{bmatrix}
Here’s the general form of gradient descent: \vec x^{(1)} = \vec{x}^{(0)} - \alpha \nabla g(\vec{x}^{(0)})
We can substitute \alpha = \frac{1}{2} and x^{(0)} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} to get: \vec x^{(1)} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} - \frac{1}{2} \nabla g(\vec x ^{(0)}) \vec x^{(1)} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} - \frac{1}{2} \begin{bmatrix} -8 \\ 0 \end{bmatrix}
\vec{x}^{(1)} = \begin{bmatrix} -1 \\ 1 \end{bmatrix} - \frac{1}{2} \begin{bmatrix} -8 \\ 0 \end{bmatrix} = \begin{bmatrix} 3 \\ 1 \end{bmatrix}
Consider the function f(t) = (t - 3)^2 + (t^2 - 1)^2. Select the true statement below.
f(t) is convex and has a global minimum.
f(t) is not convex, but has a global minimum.
f(t) is convex, but doesn’t have a global minimum.
f(t) is not convex and doesn’t have a global minimum.
f(t) is not convex, but has a global minimum.
It is seen that f(t) isn’t convex, which can be verified using the second derivative test: f'(t) = 2(t - 3) + 2(t^2 - 1) 2t = 2t - 6 + 4t^3 - 4t = 4t^3 - 2t - 6 f''(t) = 12t^2 - 2
Clearly, f''(t) < 0 for many values of t (e.g. t = 0), so f(t) is not always convex.
However, f(t) does have a global minimum – its output is never less than 0. This is because it can be expressed as the sum of two squares, (t - 3)^2 and (t^2 - 1)^2, respectively, both of which are greater than or equal to 0.
Source: Spring 2024 Final, Problem 6
Atlanta, Detroit, and Minneapolis are the three largest hub airports for Delta Airlines. You survey a sample of n students at UCSD, and find that:
20 students have been to Atlanta.
16 students have been to Detroit.
10 students have been to Minneapolis.
1 student hasn’t been to any of these three cities.
Of the 10 students who have been to Minneapolis, none have been to Detroit and 5 have been to Atlanta.
Suppose you select one student at random from your sample of n.
Suppose the event that the selected student has been to Atlanta and the event that the selected student has been to Detroit are independent.
What is the value of n? Your answer should be an integer.
32.
There are a few ways to approach the problem, all of which involve a similar sequence of calculations – specifically, the principle of inclusion-exclusion for 3 sets.
The key is remembering that there are two unknowns: the number of people overall, n, and the number of people who have been to both Atlanta and Detroit, which we’ll call k.
Many students drew Venn Diagrams, but ultimately they don’t help answer the question directly; one needs to use the independence between Atlanta and Detroit.
One way to proceed is:
1 = \frac{20}{n} + \frac{16}{n} + \frac{10}{n} + \frac{1}{n} - \frac{5}{n} - \frac{k}{n},
where \frac{k}{n} = \frac{20}{n} \cdot \frac{16}{n}. This is the key step!
Simplifying gives 1 = \frac{42}{n} - \frac{320}{n^2}, which is equivalent to n^2 - 42n + 320 = 0.
This factors into (n - 32)(n - 10) = 0, so n = 32.
Now, suppose the event that the selected student has been to Atlanta and the event that the selected student has been to Detroit are not independent, meaning that n is no longer necessarily your answer from part (a).
The event that the selected student has been to Atlanta and the event that the selected student has been to Minneapolis are conditionally independent given that the selected student has not been to Detroit.
Now, what is the value of n?
12
28
30
32
42
45
56
28.
Without any assumptions on the value of k, the number of people who have been to Atlanta and Detroit, it can be shown that:
n = 42 - k
Using the conditional independence assumption given in this part, we have that \frac{20-k}{n - 16} \cdot \frac{10}{n - 16} = \frac{5}{n - 16}, which simplifies to 2(20 - k) = n - 16 \implies n = 56 - 2k.
We now have a system of equations: \begin{cases} n = 42 - k \\ n = 56 - 2k \end{cases}
Solving this system of equations for n gives n = 28.
Consider the events A, D, and M, defined as follows:
A: The event that the selected student has been to Atlanta.
D: The event that the selected student has been to Detroit.
M: The event that the selected student has been to Minneapolis.
Let A^c, D^c, and M^c represent the complements of events A, D, and M, respectively. (In class, we used \bar{A} to represent the complement, but that’s hard to read on the exam.)
Which of the following combinations of sets form a partition of the sample space?
A D M
A \cap D^c \cap M^c D M
A \cap D D^c A^c \cap D \cap M^c
A^c A \cap D A \cap M
None of the above.
Option 3 is correct (A \cap D D^c A^c \cap D \cap M^c).
Source: Spring 2024 Final, Problem 7
Delta has released a line of trading cards. Each trading card has a picture of a plane and a color. There are 12 plane types, and for each plane type there are three possible colors (gold, silver, and platinum), meaning there are 36 trading cards total.
After your next flight, a pilot hands you a set of 6 cards, drawn at random without replacement from the set of 36 possible cards. The order of cards in a set does not matter.
In this question, you may leave your answers unsimplified, in terms of fractions, exponents, the permutation formula P(n, k), and the binomial coefficient {n \choose k}.
How many sets of 6 cards are there in total?
{36 \choose 6} = \frac{36!}{6!30!} = \frac{36 \cdot 35 \cdot 34 \cdot 33 \cdot 32 \cdot 31}{6!} = \frac{P(36, 6)}{6!}. Any of these answers, or anything equivalent to them, are correct.
There are 36 cards, and we must choose of 6 of them at random without replacement such that order matters.
How many sets of 6 cards have exactly 6 unique plane types?
{12 \choose 6} \cdot 3^6. Anything equivalent to this answer is also correct.
Since we’re asking for the number of hands with unique types, we first pick 6 different types, which can be done {12 \choose 6} ways. Then, for each chosen type, there are {3 \choose 1} = 3 ways of selecting the color. So, the colors can be chosen in 3 \cdot 3 \cdot ... \cdot 3 = 3^6 ways.
How many sets of 6 cards have exactly 2 unique plane types?
{12 \choose 2} = 66. Anything equivalent to this answer is also correct.
Once we pick 2 unique plane types, we need to choose 3 different colors per type, out of a set of 3 possibilities. This can be done, for each type, in {3 \choose 3} = 1 way.
How many sets of 6 cards have exactly 3 unique plane types, such that each plane type appears twice?
{12 \choose 3} \cdot {3 \choose 2}^3 = {12 \choose 3} 3^3. Anything equivalent to this answer is also correct.
First, we choose 3 distinct types, which can be done in ${12 \choose 3} ways. Then, for each type, we choose 2 colors, which can be done in {3 \choose 2} ways per type.
How many sets of 6 cards have exactly 3 unique plane types?
Hint: You’ll need to consider multiple cases, one of which you addressed in part (d).
{12 \choose 3} \cdot {3 \choose 2}^3 + {12 \choose 1}{11 \choose 1}{3 \choose 2}{10 \choose 1}{3 \choose 1}. Anything equivalent to this answer is also correct.
If we select 6 cards and end up with 3 unique plane types, there are two possibilities: - We get 2 of each type (e.g. xx yy zz). This is the case in part (d), so the total number of sets of 6 cards that fall here are {12 \choose 3} \cdot {3 \choose 2}^3. - We get 3 of one type, 2 of another, and 1 of the last one (e.g. xxx yy z). - xxx: There are 12 options for the type that appears 3 times, so that can be selected in {12 \choose 1} ways. We must take all 3 of that types colors, which can be done in {3 \choose 3} = 1 way. - yy: There are now 11 options for the type that appears 2 times, and for that type, we must take 2 of its three colors, so there are {11 \choose 1}{3 \choose 2} options. - z: There are now 10 options for the type that appears once, and for that type, we must take 1 of its three colors, so there are {10 \choose 1}{3 \choose 1} options. - So, the total number of options for this case is {12 \choose 1}{11 \choose 1}{3 \choose 2}{10 \choose 1}{3 \choose 1} = P(12, 3) 3^2 = {12 \choose 3} 3^3 \cdot 2.
So, the total number of options is {12 \choose 3} \cdot {3 \choose 2}^3 + {12 \choose 1}{11 \choose 1}{3 \choose 2}{10 \choose 1}{3 \choose 1}, which can be simplified in various ways, including to {12 \choose 3}3^4. Any of these ways received full credit, as long as they showed all work and logic.
Source: Spring 2024 Final, Problem 8
Delta has released a line of trading cards. Each trading card has a picture of a plane and a color. There are 12 plane types, and for each plane type there are three possible colors (gold, silver, and platinum), meaning there are 36 trading cards total.
Now, suppose that each time you board a flight, a pilot hands you 1 card drawn at random from the set of possible cards. You fly 9 times, which gives you 9 cards drawn at random with replacement from the set of possible cards.
In this question, you may leave your answers unsimplified, in terms of fractions, exponents, the permutation formula P(n, k), and the binomial coefficient {n \choose k}.
Given that you receive a gold-colored card at least once, what is the probability that you receive a gold-colored card exactly 5 times? Show your work, and put a \boxed{\text{box}} around your final answer.
\displaystyle\frac{{9 \choose 5} \left( \frac{1}{3} \right)^5 \left( \frac{2}{3} \right)^4}{1 - \left( \frac{2}{3} \right)^9}. Anything equivalent to this answer received full credit.
This boils down to recognizing that P(\text{exactly 5 gold cards | at least one gold card}) = \frac{P(\text{exactly 5 gold cards})}{P(\text{at least one gold card})}, then breaking down the numerator and denominator.
The numerator, P(\text{exactly 5 gold cards}), is equal to {9 \choose 5} \left( \frac{1}{3} \right)^5 \left( \frac{2}{3} \right)^4.
The denominator, P(\text{at least one gold card}), is equal to 1 - P(\text{no gold cards}) = 1 - \left( \frac{2}{3} \right)^9.
The Airbus A350, the Boeing 767, and the Airbus A330 are 3 of the 12 plane types that Delta made trading cards for.
What is the probability that you receive 2 Airbus A350 cards, 4 Boeing 767 cards, and 3 Airbus A330 cards? Show your work, and put a \boxed{\text{box}} around your final answer.
\displaystyle\frac{9!}{2!4!3!} (\frac{1}{12})^9. Anything equivalent to this answer received full credit, such as ${9 }{5 }{3 } ()^9 $ or {9 \choose 3}{6 \choose 4} (\frac{1}{12})^9.
On one individual draw, the probability of receiving one particular plane type is \frac{3}{36} = \frac{1}{12}, so the probability of seeing a particular sequence of 9 plane types – like A350, B767, A330, A330, B767, A350, A330, B767, B767 – is (\frac{1}{12})^9.
But, we need to account for the number of ways we can arrange 2 A350, 4 B767, and 3 A330 cards, which is \frac{9!}{2!4!3!} = {9 \choose 2} {7 \choose 4}{3 \choose 3} (which can also be expressed a few other ways, too).
Source: Spring 2024 Final, Problem 9
Delta’s flight operations center keeps track of weather conditions, as they tend to impact whether or not flights are late. For each flight, Delta keeps track of:
Whether or not there was precipitation — i.e., rain, snow, or hail.
The wind conditions — either no winds, light winds, moderate winds, or heavy winds.
The flight’s status — whether it was early, on time, or late.
Information about 100 flights is summarized in the table below.
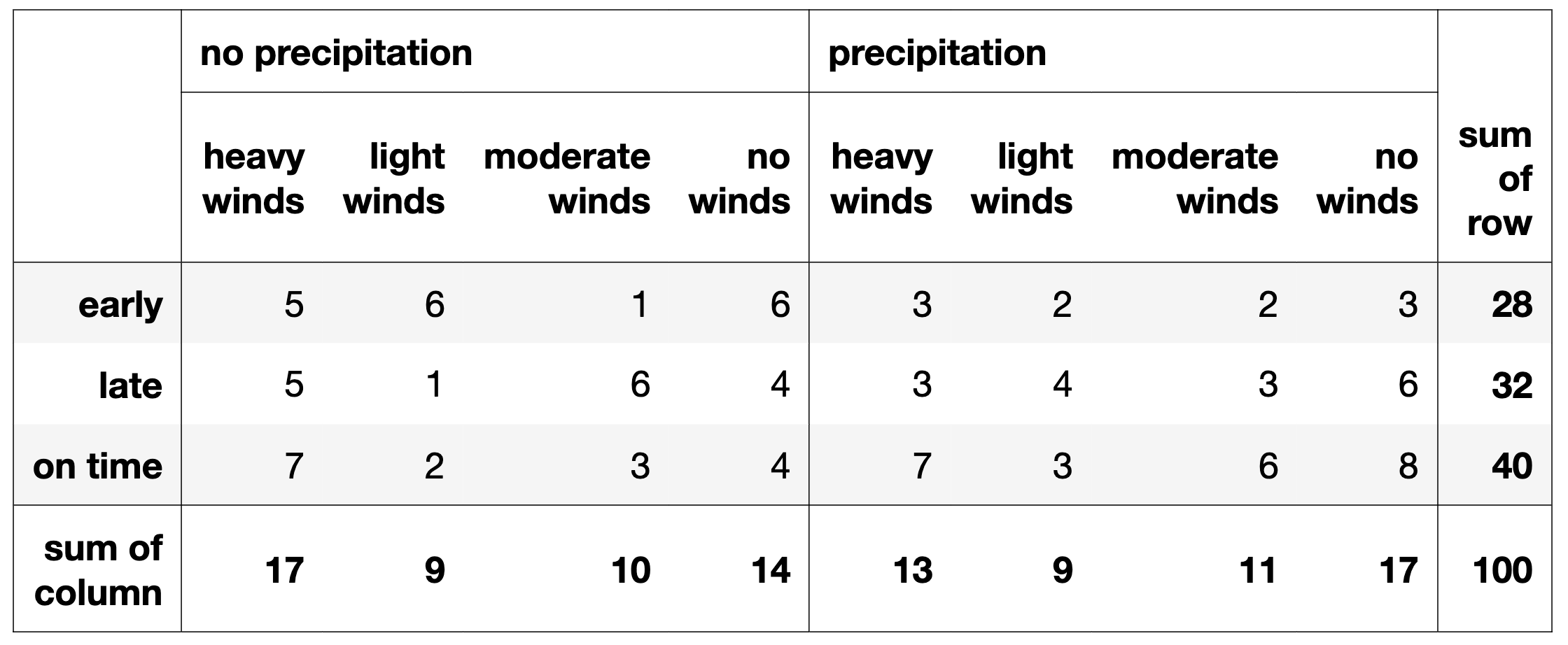
For instance, we’re told that 6 flights in moderate winds and no precipitation landed late, and that there were 13 total flights in heavy winds and precipitation.
Delta would like to use this information to predict whether a new flight will be early, on time, or late, given the weather conditions.
Without smoothing, what is:
\mathbb{P}(\text{heavy winds} \: | \: \text{early})
\frac{2}{7}
\frac{5}{7}
\frac{3}{8}
\frac{3}{10}
\frac{14}{15}
\frac{3}{28}
\frac{5}{28}
\frac{2}{7}.
There are 28 flights that landed early, and of those, 5 + 3 = 8 were in heavy winds, which means our estimate is \frac{8}{28} = \frac{2}{7}.
With smoothing, what is:
\mathbb{P}(\text{heavy winds} \: | \: \text{early})
\frac{1}{3}
\frac{3}{8}
\frac{3}{11}
\frac{9}{29}
\frac{9}{32}
\frac{31}{101}
\frac{31}{104}
\frac{9}{32}.
There are 28 flights that landed early, and of those, 5 + 3 = 8 were in heavy winds, which means our estimate is \displaystyle\frac{8+1}{28+4} = \frac{9}{32}. (The denominator is 28 + 4 since there are 4 possible wind conditions – none, light, moderate, and heavy.)
For your convenience, the table from the previous page is repeated again below.

An airline’s late-to-early ratio, given a set of weather conditions, is defined as:
\frac{\mathbb{P}(\text{late} \: | \: \text{conditions})}{\mathbb{P}(\text{early} \: | \: \text{conditions})}
Using the assumptions of the Naïve Bayes classifier without smoothing, show that Delta’s late-early ratio for flights in heavy winds and precipitation is \bf{\frac{7}{5}}.
Hint: You’ll end up needing to compute 6 probabilities, one of which you already found in part (a).
We can recognize that:
\displaystyle\frac{P(\text{late | conditions})}{P(\text{early | conditions})} \\ = \displaystyle\frac{P(\text{late}) \cdot P(\text{heavy winds | late}) \cdot P(\text{precipitation | late})}{P(\text{early}) \cdot P(\text{heavy winds | early}) \cdot P(\text{precipitation | early})}
and compute the following:
P(\text{late}) = \frac{32}{100}
P(\text{heavy winds | late}) = \frac{8}{32}
P(\text{precipitation | late}) = \frac{16}{32}
P(\text{early}) = \frac{28}{100}
P(\text{heavy winds | early}) = \frac{8}{28}
P(\text{precipitation | early}) = \frac{10}{28}
which gives:
\displaystyle\frac{\displaystyle\frac{32}{100} \cdot \displaystyle\frac{8}{32} \cdot \displaystyle\frac{16}{32}}{\displaystyle\frac{28}{100} \cdot \displaystyle\frac{8}{28} \cdot \displaystyle\frac{10}{28}} = \displaystyle\frac{\displaystyle\frac{1}{25}}{\displaystyle\frac{1}{35}} = \displaystyle\frac{7}{5}.