← return to practice.dsc40a.com
This page contains all problems about Matrices, Vectors, and their Properties.
Source: Summer Session 2 2024 Final, Problem 3a-g
Consider the following vectors in \mathbb{R}^3, where \alpha \in \mathbb{R} is a scalar:
\vec{v}_1 = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix}, \quad \vec{v}_2 = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}, \quad \vec{v}_3 = \begin{bmatrix} \alpha \\ 1 \\ 2 \end{bmatrix}
For what value(s) of \alpha are \vec{v}_1, \vec{v}_2, and \vec{v}_3 linearly independent? Show your work, and put your answer in a box.
The vectors are linearly independent for any \alpha \neq 1.
To be linearly independent it means there is not a linear combination between any of the vectors. We can see that if we add \vec v_1 and \vec v_2 it looks almost like \vec v_3, so as long as we can make it so \alpha \neq 1 then the vectors will be independent.
The average score on this problem was 69%.
For what value(s) of \alpha are \vec{v}_1 and \vec{v}_3 orthogonal? Show your work, and put your answer in a box.
We know for \vec v_1 and \vec v_3 to be orthogonal their dot product should equal zero.
\vec v_1 \cdot \vec v_3 = (0)(\alpha) + (1)(1) + (1)(2) = 0
There are no values of \alpha for which \vec{v}_1, \vec{v}_3 are orthogonal. We can see (0)(\alpha) = 0, which means that we cannot manipulate \alpha in any way to make the vectors orthogonal.
The average score on this problem was 88%.
For what value(s) of \alpha are \vec{v}_2 and \vec{v}_3 orthogonal? Show your work, and put your answer in a box.
\alpha = -2
We know for \vec v_2 and \vec v_3 to be orthogonal their dot product should equal zero.
The dot product is:
\vec v_2 \cdot \vec v_3 = (1)(\alpha) + (0)(1) + (1)(2)
So we can do:
\begin{align*} 0 &= (1)(\alpha) + (0)(1) + (1)(2)\\ 0 &=\alpha + 0 + 2\\ -2 &= \alpha \end{align*}
We can clearly see when \alpha = -2 then the dot product will equal zero.
The average score on this problem was 100%.
Regardless of your answer above, assume in this part that \alpha = 3. Is the vector \begin{bmatrix} 3 \\ 5 \\ 8 \end{bmatrix} in \textbf{span}(\vec{v}_1, \vec{v}_2, \vec{v}_3)?
Yes
No
Yes
If \alpha = 3 and all three vectors are independent from one another then any vector in \mathbb{R}^3 is in the span of 3 linearly independent vectors in \mathbb{R}^3.
The average score on this problem was 94%.
The following information is repeated from the previous page, for your convenience.
Consider the following vectors in \mathbb{R}^3, where \alpha \in \mathbb{R} is some scalar:
\vec{v}_1 = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix}, \quad \vec{v}_2 = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}, \quad \vec{v}_3 = \begin{bmatrix} \alpha \\ 1 \\ 2 \end{bmatrix}
What is the projection of the vector \begin{bmatrix} 3 \\ 5 \\ 8 \end{bmatrix} onto \vec{v}_1? Provide your answer in the form of a vector. Show your work, and put your answer in a box.
\begin{bmatrix}0 \\ 6.5 \\ 6.5 \end{bmatrix}
We follow the equation \frac{\begin{bmatrix}3 \\ 5 \\ 8\end{bmatrix} \cdot \vec v_1}{\vec v_1 \cdot \vec v_1} \vec v_1 to find the projection of \begin{bmatrix}3 \\ 5 \\ 8\end{bmatrix} onto \vec{v_1}:
\begin{align*} \frac{\begin{bmatrix}3 \\ 5 \\ 8\end{bmatrix} \cdot \begin{bmatrix}0 \\ 1 \\ 1 \end{bmatrix}}{\begin{bmatrix}0 \\ 1 \\ 1 \end{bmatrix}\cdot \begin{bmatrix}0 \\ 1 \\ 1 \end{bmatrix}} \begin{bmatrix}0 \\ 1 \\ 1 \end{bmatrix} &= \frac{13}{2} \begin{bmatrix}0 \\ 1 \\ 1 \end{bmatrix}\\ &= \begin{bmatrix}0 \\ 6.5 \\ 6.5 \end{bmatrix} \end{align*}
The average score on this problem was 58%.
The following information is repeated from the previous page, for your convenience.
Consider the following vectors in \mathbb{R}^3, where \alpha \in \mathbb{R} is some scalar:
\vec{v}_1 = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix}, \quad \vec{v}_2 = \begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}, \quad \vec{v}_3 = \begin{bmatrix} \alpha \\ 1 \\ 2 \end{bmatrix}
What is the orthogonal projection of the vector \begin{bmatrix} 3 \\ 15 \\ 18 \end{bmatrix} onto \textbf{span}(\vec{v}_1, \vec{v}_2)? Note that for X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ 1 & 1 \end{bmatrix}, we have
(X^T X) ^{-1}X^T = \begin{bmatrix} -\frac{1}{3} & \frac{2}{3} & \frac{1}{3} \\[6pt] \frac{2}{3} & -\frac{1}{3} & \frac{1}{3} \end{bmatrix} Write your answer in the form of coefficients that multiply \vec{v}_1 and \vec{v}_2 and yield a vector \vec{p} that is the orthogonal projection requested above.
\vec{p} = \_\_(a)\_\_ \cdot \vec{v}_1 + \_\_(b)\_\_ \cdot \vec{v}_2
What goes in \_\_(a)\_\_ and \_\_(b)\_\_?
To find what goes in \_\_(a)\_\_ and \_\_(b)\_\_ we need to multiply (X^T X)^{-1}X^T and \vec y.
\begin{align*} \begin{bmatrix} a \\ b \end{bmatrix} &= (X^T X)^{-1}X^T \begin{bmatrix}3 \\ 15 \\ 18\end{bmatrix}\\ \begin{bmatrix} a \\ b \end{bmatrix} &= \begin{bmatrix} -\frac{1}{3}(3) & \frac{2}{3}(15) & \frac{1}{3}(18) \\ \frac{2}{3}(3) & -\frac{1}{3}(15) & \frac{1}{3}(18) \end{bmatrix}\\ \begin{bmatrix} a \\ b \end{bmatrix} &= \begin{bmatrix} -1 + 10 + 15 \\ 2 - 5 + 6 \end{bmatrix}\\ \begin{bmatrix} a \\ b \end{bmatrix} &= \begin{bmatrix} 15 \\ 3 \end{bmatrix}\\ \end{align*}
The average score on this problem was 73%.
Is it true that, for the orthogonal projection \vec{p} from above, the entries of \vec{e} = \vec{p} \ - \begin{bmatrix} 3 \\ 15 \\ 18 \end{bmatrix} sum to 0? Explain why or why not. Your answer must mention characteristics of \vec{v}_1,\vec{v}_2, and/or X to receive full credit.
Yes
No
Explain your answer
Yes
Note: Design matrix X lacks a column of all 1s (and the span of its columns does not include all 1s), so residuals don’t necessarily not sum to 0. This means we need more evidence!
\vec{p} is the orthogonal projection of \begin{bmatrix}3\\15\\18\end{bmatrix} onto \text{span}(\vec{v_1}, \vec{v_2}) where \vec{v_1} and \vec{v_2} are the column of the matrix X. From the instructions we know: \vec{e} = \vec{p} \ - \begin{bmatrix} 3 \\ 15 \\ 18 \end{bmatrix}. This means if \begin{bmatrix}3\\15\\18\end{bmatrix} lies in \text{span}(\vec{v_1}, \vec{v_2}) then \vec{e} = \vec{0}. We know \vec{p} is exactly \begin{bmatrix}3\\15\\18\end{bmatrix}, which means the sum of residuals equals 0.
The average score on this problem was 69%.
Source: Summer Session 2 2024 Midterm, Problem 2a-b
Prove the following statement or provide a counterexample:
If a vector \vec{v} is orthogonal to a vector \vec{w}, then \vec{v} is also orthogonal to the projection of an arbitrary vector \vec{u} onto \vec{w}.
The statement above is true.
Let the following information hold:
When a vector is orthogonal to another their dot product will equal zero. This means \vec{v} \cdot \vec{w} = 0.
From lecture we know: c\vec{w} = \frac{\vec{w} \cdot \vec{u}}{\vec{w} \cdot \vec{w}} \cdot \vec{w}
So, now we can solve c\vec{w} \cdot \vec{v} = \frac{\vec{w} \cdot \vec{u} \cdot \vec{w} \cdot \vec{v}}{\vec{w} \cdot \vec{w}}. The numerator becomes zero because \vec{v} \cdot \vec{w} = 0 and anything multiplied by zero will also be zero. This means the projection of \vec{u} onto \vec{w} is orthogonal to \vec v.
The average score on this problem was 52%.
If a vector \vec{v} is orthogonal to a vector \vec{w}, then \vec{v} is also orthogonal to the projection of \vec{w} onto an arbitrary vector \vec{u}.
The statement above is false.
Let the following hold:
Let’s check if \vec w \cdot \vec v = 0. (1)(-2)+(1)(2) = 0 That worked! Now we can calculate the projection of \vec w onto \vec u.
\begin{align*} \frac{\vec w \cdot \vec u}{\vec u \cdot \vec u}\vec u &= \frac{(-2)(0)+(1)(1)}{(0)(0)+(1)(1)} \cdot \begin{bmatrix} 0 \\ 1 \end{bmatrix}\\ &= -1 \cdot \begin{bmatrix} 0 \\ 1 \end{bmatrix}\\ &= \begin{bmatrix} 0 \\ -1 \end{bmatrix} \end{align*}
Now we can check to see if \vec v \cdot the projection of \vec w onto \vec u is equal to zero.
\begin{align*} &\begin{bmatrix} 0 \\ -1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \end{bmatrix}\\ &= (0)(1) + (2)(-1) = -1\\ &\text{and } -1 \neq 0 \end{align*}
We can see that \vec v \cdot the projection of \vec w onto \vec u is not equal to zero.
The average score on this problem was 50%.
Source: Summer Session 2 2024 Midterm, Problem 2c
Consider the following information:
Select the dimensionality of each of the objects below:
M \vec{v}
An n \times n matrix.
An m \times m matrix.
An n \times m matrix.
An m-dimensional vector.
An n-dimensional vector.
A scalar.
Invalid operation.
An m-dimensional vector.
We know the following information:
This means:
M = \begin{bmatrix} & & \\ & & \\ & & \\ \end{bmatrix}_{m \times n} \text{ and } \vec{v} = \begin{bmatrix} & \\ & \\ \end{bmatrix}_{n \times 1}
When you multiply M \vec{v} the n will both cancel out leaving you with an object with the size \begin{bmatrix}& \\& \\& \\\end{bmatrix}_{m \times 1}, which is an m-dimensional vector.
The average score on this problem was 87%.
M^T M
An n \times n matrix.
An m \times m matrix.
An n \times m matrix.
An m-dimensional vector.
An n-dimensional vector.
A scalar.
Invalid operation.
An n \times n matrix.
We know the following information:
This means:
M^T = \begin{bmatrix} & & & \\ & & & \\ \end{bmatrix}_{n \times m} \text{ and } M = \begin{bmatrix} & & \\ & & \\ & & \\ \end{bmatrix}_{m \times n}
When you multiply M^T M the m will both cancel out leaving you with an object with the size \begin{bmatrix}& & \\& & \\\end{bmatrix}_{n \times n}, which is an n \times n matrix.
The average score on this problem was 87%.
\vec{v}^T N \vec{v}
An n \times n matrix.
An m \times m matrix.
An n \times m matrix.
An m-dimensional vector.
An n-dimensional vector.
A scalar.
Invalid operation.
A scalar.
We know the following information:
This means:
\vec{v}^T = \begin{bmatrix} & & \end{bmatrix}_{1 \times n} \text{, } N = \begin{bmatrix} & & \\ & & \\ \end{bmatrix}_{n \times n} \text{, and } \vec{v} = \begin{bmatrix} & \\ & \\ \end{bmatrix}_{n \times 1}
When you multiply \vec{v}^T N the n will both cancel out leaving you with an object with the size \begin{bmatrix}& &\end{bmatrix}_{1 \times n}. When you multiply this object by \vec{v} the n will cancel out again leaving you with an object with the size \begin{bmatrix}&\end{bmatrix}_{1 \times 1}, which is a scalar.
The average score on this problem was 93%.
N \vec{v} + s \vec{v}
An n \times n matrix.
An m \times m matrix.
An n \times m matrix.
An m-dimensional vector.
An n-dimensional vector.
A scalar.
Invalid operation.
An n-dimensional vector.
We know the following information:
This means:
\vec{v} = \begin{bmatrix} & \\ & \\ \end{bmatrix}_{n \times 1} \text{, } N = \begin{bmatrix} & & \\ & & \\ \end{bmatrix}_{n \times n} \text{, and } s = \begin{bmatrix} & \end{bmatrix}_{1 \times 1}
When you multiply N \vec{v} the n will both cancel out leaving you with an object with the size \begin{bmatrix}& \\& \\\end{bmatrix}_{n \times 1}. When you multiply s \vec{v} the dimensions of \vec{v} does not change, so you will have an object with the size \begin{bmatrix}& \\& \\\end{bmatrix}_{n \times 1}. When you add these vectors the dimension will not change, so you are left with an n-dimensional vector.
The average score on this problem was 87%.
M^T M \vec{v}
An n \times n matrix.
An m \times m matrix.
An n \times m matrix.
An m-dimensional vector.
An n-dimensional vector.
A scalar.
Invalid operation.
An n-dimensional vector.
We know the following information:
This means:
M^T = \begin{bmatrix} & & & \\ & & & \\ \end{bmatrix}_{n \times m} \text{, } M = \begin{bmatrix} & & \\ & & \\ & & \\ \end{bmatrix}_{m \times n} \text{, and } \vec{v} = \begin{bmatrix} & \\ & \\ \end{bmatrix}_{n \times 1}
When you multiply M^T M the m will both cancel out leaving you with an object with the size \begin{bmatrix}& & \\& & \\\end{bmatrix}_{n \times n}, which is an n \times n matrix.
When you multiply \begin{bmatrix}& & \\& & \\\end{bmatrix}_{n \times n} \times \begin{bmatrix}& \\&\\\end{bmatrix}_{n \times 1} the n will cancel out leaving you with an n-dimensional vector.
The average score on this problem was 81%.
Source: Summer Session 2 2024 Midterm, Problem 2d
Consider the following information:
If \vec{e} is orthogonal to every column in A, prove that \vec{b} must satisfy the following equation:
A^T A \vec{b} = A^T \vec{d}.
Hint: If the columns of a matrix A are orthogonal to a vector \vec{v}, then A^T \vec{v} = 0.
To begin with, we know from the bullet points above that A^T \vec e = 0 in order for A^T A \vec{b} = A^T \vec{d} to be true. So we start by interpreting A^T \vec e = 0 in \vec e’s other form \vec{d} - \vec{c}. We get A^T(\vec d - \vec c)!
We then distribute A^T to get A^T \vec d - A^T \vec c = 0. From here we can move A^T \vec c to the right to get A^T \vec d = A^T \vec c.
From the third bullet point we find \vec c = A\vec{b}, so we can write A^T \vec d = A^T A \vec b. Thus we have proved if \vec{e} is orthogonal to every column in A that \vec{b} must satisfy the following equation: A^T A \vec{b} = A^T \vec{d}.
The average score on this problem was 58%.
Source: Summer Session 2 2024 Midterm, Problem 3a
Fill in the blanks for each set of vectors below to accurately describe their relationship and span.
\vec{a} = \begin{bmatrix} 1 \\ 3 \end{bmatrix} \qquad \vec{b} = \begin{bmatrix} -2 \\ 1 \end{bmatrix}
“\vec{a} and \vec{b} are __(i)__, meaning they span a __(ii)__. The vector \vec{c} = \begin{bmatrix} -6 \\ 11 \end{bmatrix} __(iii)__ in the span of \vec{a} and \vec{b}. \vec{a} and \vec{b} are __(iv)__, meaning the angle between them is __(v)__”
What goes in __(i)__?
linearly independent
linearly dependent
Linearly Independent
Vectors \vec{a} and \vec{b} are linearly independent because they aren’t multiples of each other. They each point in different (but not opposite) directions, so we can’t express either vector as a scalar multiple of the other.
The average score on this problem was 81%.
What goes in __(ii)__?
line
plane
cube
unknown
Plane
Any two linearly independent vectors must span a plane. Geometrically, we can think of all scalar multiples of a single vector to lie along a single line. Then, linear combinations of any two vectors pointing in different directions must lie on the same plane.
The average score on this problem was 81%.
What goes in __(iii)__?
is
is not
may be
is
A quick way to know that \vec{c} lies in the span of \vec{a} and \vec{b} is because we are dealing with 2-dimensional vectors and we know that \vec{a} and \vec{b} span a plane (so they must span all of \mathbb{R}^2). \vec{c} exists in 2-dimensional space, so it must exist in the span of \vec{a} and \vec{b}.
We can also directly check if \vec{c} lies in the span of \vec{a} and \vec{b} if there exists some constants c_1 and c_2 such that c_1 \vec{a} + c_2 \vec{b} = \vec{c}. Plugging in what we know: c_1 \begin{bmatrix} 1 \\ 3 \end{bmatrix} + c_2 \begin{bmatrix} -2 \\ 1 \end{bmatrix} = \begin{bmatrix} -6 \\ 11 \end{bmatrix} This gives us the system of equations: c_1 (1) + c_2 (-2) = -6 c_1 (3) + c_2 (1) = 11 Solving this system gives us c_1 = \frac{16}{7}, c_2 = \frac{29}{7}, which means \vec{c} does lie in the span of \vec{a} and \vec{b}.
The average score on this problem was 68%.
What goes in __(iv)__?
orthogonal
collinear
neither orthogonal nor collinear
neither orthogonal nor collinear
The vectors \vec{a} and \vec{b} are orthogonal if \vec{a} \cdot \vec{b} = 0. We can compute \vec{a} \cdot \vec{b} = (1)(-2) + (3)(1) = 1 \neq 0, so \vec{a} and \vec{b} are not orthogonal.
The vectors \vec{a} and \vec{b} are collinear if we can write one vector as a scalar multiple of the other. But we already know \vec{a} and \vec{b} are linearly independent, so they don’t lie along the same line and aren’t collinear.
The average score on this problem was 68%.
What goes in __(v)__?
0 or 180 degrees
something else
90 degrees
something else
If two vectors are orthogonal, the angle between them is 90 degrees. If two vectors are collinear, the angle between them is 0 or 180 degrees. Since \vec{a} and \vec{b} are neither of these, then the angle between them must be something else.
The average score on this problem was 81%.
Source: Summer Session 2 2024 Midterm, Problem 3b
Fill in the blanks for each set of vectors below to accurately describe their relationship and span.
\vec{a} = \begin{bmatrix} -2 \\ 1.5 \\ 4 \end{bmatrix} \qquad \vec{b} = \begin{bmatrix} 1 \\ 2 \\ -2.5 \end{bmatrix} \qquad \vec{c} = \begin{bmatrix} -6 \\ 10 \\ 11 \end{bmatrix}
“\vec{a}, \vec{b}, and \vec{c} are __(i)__, meaning they span a __(ii)__. The vector \vec{a} = \begin{bmatrix} -2 \\ 15 \\ -7 \end{bmatrix} __(iii)__ in the span of \vec{a}, \vec{b}, and \vec{c}. \vec{a}, \vec{b}, and \vec{c} are __(iv)__, meaning the angle between them is __(v)__”
What goes in __(i)__?
linearly independent
linearly dependent
Linearly Dependent
To check if \vec{a}, \vec{b}, \vec{c} are linearly independent or dependent, it is possible to try a few different linear combinations of two vectors, and see if it equals the third vector. In this case, we can see that 4\vec{a} + 2\vec{b} = \vec{c}, so they are linearly dependent. For a more straight-forward computation, we can arrange these vectors as the columns of a matrix and compute their rank: A = \begin{bmatrix} -2 & 1 & -6 \\ 1.5 & 2 & 10 \\ 4 & -2.5 & 11\end{bmatrix} Then, we can perform row operations to reduce the matrix A. This gives us RREF(A) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0\end{bmatrix} From here, we see that there only two columns with leading 1s, which implies the vectors are linearly dependent.
The average score on this problem was 94%.
What goes in __(ii)__?
line
plane
cube
unknown
Plane
We know from above that the three vectors are linearly dependent. It is clear that they all do not lie on the same line, since we can’t multiply any single vector by a constant to obtain another vector. If all three vectors were independent, they would span all of \mathbb{R}^3, or 3-dimensional space. Since this isn’t the case, they must span a plane.
The average score on this problem was 63%.
What goes in __(iii)__?
is
is not
may be
is not
If \vec{d} was in the span of \vec{a}, \vec{b}, \vec{c}, then there should exist constants to fulfill the equation: c_1 \vec{a} + c_2 \vec{b} + c_3 \vec{c} = \vec{d} We can set this up as an augmented matrix: A = \begin{bmatrix} -2 & 1 & -6 & -2 \\ 1.5 & 2 & 10 & 15 \\ 4 & -2.5 & 11 & -7 \end{bmatrix} After performing row operations, we obtain: RREF(A) = \begin{bmatrix} 1 & 0 & 4 & 0 \\ 0 & 1 & 2 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix} This tells us our system of equations is inconsistent because the last row implies 0=1. Therefore, there does not exist a solution, and \vec{d} is not in the span of \vec{a}, \vec{b}, \vec{c}.
The average score on this problem was 50%.
What goes in __(iv)__?
orthogonal
collinear
neither orthogonal nor collinear
neither orthogonal nor collinear
We can tell that \vec{a}, \vec{b}, \vec{c} are not collinear because their span isn’t a line. In order to check if these vectors are orthogonal, we can compute the dot product between each pair of vectors; if any of the three dot products are not equal to 0, then they are not orthogonal.
We see that \vec{a} \cdot \vec{b} = (-2)(1) + (1.5)(2) + (4)(-2.5) = -9 \neq 0, so the three vectors together are not orthogonal.
The average score on this problem was 81%.
What goes in __(v)__?
0 or 180 degrees
something else
90 degrees
something else
If two vectors are orthogonal, the angle between them is 90 degrees. If two vectors are collinear, the angle between them is 0 or 180 degrees. Since each pair of the vectors \vec{a}, \vec{b}, \vec{c} are neither of these, then the angles between them must be something else.
The average score on this problem was 81%.
Source: Summer Session 2 2024 Midterm, Problem 3c
Fill in the blanks for each set of vectors below to accurately describe their relationship and span.
\vec{a} = \begin{bmatrix} -1 \\ 4 \end{bmatrix} \qquad \vec{b} = \begin{bmatrix} 0.5 \\ -2 \end{bmatrix}
“\vec{a} and \vec{b} are __(i)__, meaning they span a __(ii)__. The vector \vec{c} = \begin{bmatrix} -3 \\ 4 \end{bmatrix} __(iii)__ in the span of \vec{a} and \vec{b}. \vec{a} and \vec{b} are __(iv)__, meaning the angle between them is __(v)__”
What goes in __(i)__?
linearly independent
linearly dependent
Linearly Dependent
Upon inspection, we can see that \vec{b} = -\frac{1}{2}\vec{a}. Therefore, these vectors are linearly dependent.
The average score on this problem was 81%.
What goes in __(ii)__?
line
plane
cube
unknown
Line
Since we found that \vec{a} and \vec{b} are linearly dependent, they must span a space of only 1-dimension. This means that \vec{a} and \vec{b} lie the same line.
The average score on this problem was 87%.
What goes in __(iii)__?
is
is not
may be
is not
We know that \vec{a} and \vec{b} span a line consisting only of vectors that are scalar multiples of \vec{a} or \vec{b}. We can see that the first component of \vec{c} is three times larger than the first component of \vec{a}, but they both share the same second component. This means it is not possible to scale \vec{a} by a constant to obtain \vec{c}, and so \vec{c} does not lie on the same line spanned by \vec{a} and \vec{b}.
The average score on this problem was 93%.
What goes in __(iv)__?
orthogonal
collinear
neither orthogonal nor collinear
Collinear
The vectors \vec{a} and \vec{b} are collinear if we can write one vector as a scalar multiple of the other. We saw that \vec{b} = -\frac{1}{2}\vec{a}, so they are collinear.
The average score on this problem was 62%.
What goes in __(v)__?
0 or 180 degrees
something else
90 degrees
0 or 180 degrees
If two vectors are collinear, the angle between them is 0 or 180 degrees. This is because they lie on the same line and either point in the same or opposite directions from the origin.
The average score on this problem was 81%.
Source: Summer Session 2 2024 Midterm, Problem 3d
Fill in the blanks for each set of vectors below to accurately describe their relationship and span.
\vec{a} = \begin{bmatrix} -3 \\ -2 \end{bmatrix} \qquad \vec{b} = \begin{bmatrix} -2 \\ 3 \end{bmatrix}
“\vec{a} and \vec{b} are __(i)__, meaning they span a __(ii)__. The vector \vec{a} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} __(iii)__ in the span of \vec{a} and \vec{b}. \vec{a} and \vec{b} are __(iv)__, meaning the angle between them is __(v)__”
What goes in __(i)__?
linearly independent
linearly dependent
Linearly Independent
We can see that one vector is not a scalar multiple of the other. \vec{a} has both negative components, so we would only be able to obtain scalar multiples with both negative or both positive components. On the other hand, \vec{b} has one negative and one positive component. So they must be linearly independent.
The average score on this problem was 75%.
What goes in __(ii)__?
line
plane
cube
unknown
Plane
Any two linearly independent vectors must span a plane. Geometrically, we can think of all scalar multiples of a single vector to lie along a single line. Then, linear combinations of any two vectors pointing in different directions must lie on the same plane.
The average score on this problem was 87%.
What goes in __(iii)__?
is
is not
may be
is
Similar to Q5, we can tell that \vec{c} lies in the span of \vec{a} and \vec{b} because we are dealing with 2-dimensional vectors, and we know that \vec{a} and \vec{b} span a plane (so they must span all of \mathbb{R}^2). \vec{c} exists in 2-dimensional space, so it must exist in the span of \vec{a} and \vec{b}.
We can also directly check if \vec{c} lies in the span of \vec{a} and \vec{b} if there exists some constants c_1 and c_2 such that c_1 \vec{a} + c_2 \vec{b} = \vec{c}. Plugging in what we know: c_1 \begin{bmatrix} -3 \\ -2 \end{bmatrix} + c_2 \begin{bmatrix} -2 \\ 3 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$ This gives us the system of equations: c_1 (-3) + c_2 (-2) = 1 c_1 (-2) + c_2 (3) = 1 Solving this system gives us c_1 = -\frac{5}{13}, c_2 = \frac{1}{13}, which means \vec{c} does lie in the span of \vec{a} and \vec{b}.
The average score on this problem was 75%.
What goes in __(iv)__?
orthogonal
collinear
neither orthogonal nor collinear
Orthogonal
The vectors \vec{a} and \vec{b} are orthogonal if \vec{a} \cdot \vec{b} = 0. We can compute \vec{a} \cdot \vec{b} = (-3)(-2) + (-2)(3) = 6 - 6 = 0, so \vec{a} and \vec{b} are orthogonal.
The average score on this problem was 87%.
What goes in __(v)__?
0 or 180 degrees
something else
90 degrees
90 degrees
Since \vec{a} and \vec{b} are orthogonal, the angle between them is 90 degrees.
The average score on this problem was 87%.
Source: Spring 2024 Final, Problem 4
Consider the vectors \vec{u} and \vec{v}, defined below.
\vec{u} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \qquad \vec{v} = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix}
We define X \in \mathbb{R}^{3 \times 2} to be the matrix whose first column is \vec u and whose second column is \vec v.
In this part only, let \vec{y} = \begin{bmatrix} -1 \\ k \\ 252 \end{bmatrix}.
Find a scalar k such that \vec{y} is in \text{span}(\vec u, \vec v). Give your answer as a constant with no variables.
252.
Vectors in \text{span}(\vec u, \vec v) must have an equal 2nd and 3rd component, and the third component is 252, so the second must be as well.
Show that: (X^TX)^{-1}X^T = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{2} & \frac{1}{2} \end{bmatrix}
Hint: If A = \begin{bmatrix} a_1 & 0 \\ 0 & a_2 \end{bmatrix}, then A^{-1} = \begin{bmatrix} \frac{1}{a_1} & 0 \\ 0 & \frac{1}{a_2} \end{bmatrix}.
We can construct the following series of matrices to get (X^TX)^{-1}X^T.
In parts (c) and (d) only, let \vec{y} = \begin{bmatrix} 4 \\ 2 \\ 8 \end{bmatrix}.
Find scalars a and b such that a \vec u + b \vec v is the vector in \text{span}(\vec u, \vec v) that is as close to \vec{y} as possible. Give your answers as constants with no variables.
a = 4, b = 5.
The result from the part (b) implies that when using the normal equations to find coefficients for \vec u and \vec v – which we know from lecture produce an error vector whose length is minimized – the coefficient on \vec u must be y_1 and the coefficient on \vec v must be \frac{y_2 + y_3}{2}. This can be shown by taking the result from part (b), \begin{bmatrix} 1 & 0 & 0 \\ 0 & \frac{1}{2} & \frac{1}{2} \end{bmatrix}, and multiplying it by the vector \vec y = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \end{bmatrix}.
Here, y_1 = 4, so a = 4. We also know y_2 = 2 and y_3 = 8, so b = \frac{2+8}{2} = 5.
Let \vec{e} = \vec{y} - (a \vec u + b \vec v), where a and b are the values you found in part (c).
What is \lVert \vec{e} \rVert?
0
3 \sqrt{2}
4 \sqrt{2}
6
6 \sqrt{2}
2\sqrt{21}
3 \sqrt{2}.
The correct value of a \vec u + b \vec v = \begin{bmatrix} 4 \\ 5 \\ 5\end{bmatrix}. Then, \vec{e} = \begin{bmatrix} 4 \\ 2 \\ 8 \end{bmatrix} - \begin{bmatrix} 4 \\ 5 \\ 5 \end{bmatrix} = \begin{bmatrix} 0 \\ -3 \\ 3 \end{bmatrix}, which has a length of \sqrt{0^2 + (-3)^2 + 3^2} = 3\sqrt{2}.
Is it true that, for any vector \vec{y} \in \mathbb{R}^3, we can find scalars c and d such that the sum of the entries in the vector \vec{y} - (c \vec u + d \vec v) is 0?
Yes, because \vec{u} and \vec{v} are linearly independent.
Yes, because \vec{u} and \vec{v} are orthogonal.
Yes, but for a reason that isn’t listed here.
No, because \vec{y} is not necessarily in
No, because neither \vec{u} nor \vec{v} is equal to the vector
No, but for a reason that isn’t listed here.
Yes, but for a reason that isn’t listed here.
Here’s the full reason: 1. We can use the normal equations to find c and d, no matter what \vec{y} is. 2. The error vector \vec e that results from using the normal equations is such that \vec e is orthogonal to the span of the columns of X. 3. The columns of X are just \vec u and \vec v. So, \vec e is orthogonal to any linear combination of \vec u and \vec v. 4. One of the many linear combinations of \vec u and \vec v is \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}. 5. This means that the vector \vec e is orthogonal to \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}, which means that \vec{1}^T \vec{e} = 0 \implies \sum_{i = 1}^3 e_i = 0.
Suppose that Q \in \mathbb{R}^{100 \times 12}, \vec{s} \in \mathbb{R}^{100}, and \vec{f} \in \mathbb{R}^{12}. What are the dimensions of the following product?
\vec{s}^T Q \vec{f}
scalar
12 \times 1 vector
100 \times 1 vector
100 \times 12 matrix
12 \times 12 matrix
12 \times 100 matrix
undefined
Correct: Scalar.
The inner dimensions of 100 and 12 cancel, and so \vec{s}^T Q \vec{f} is of shape 1 x 1.
Source: Spring 2024 Final, Problem 1
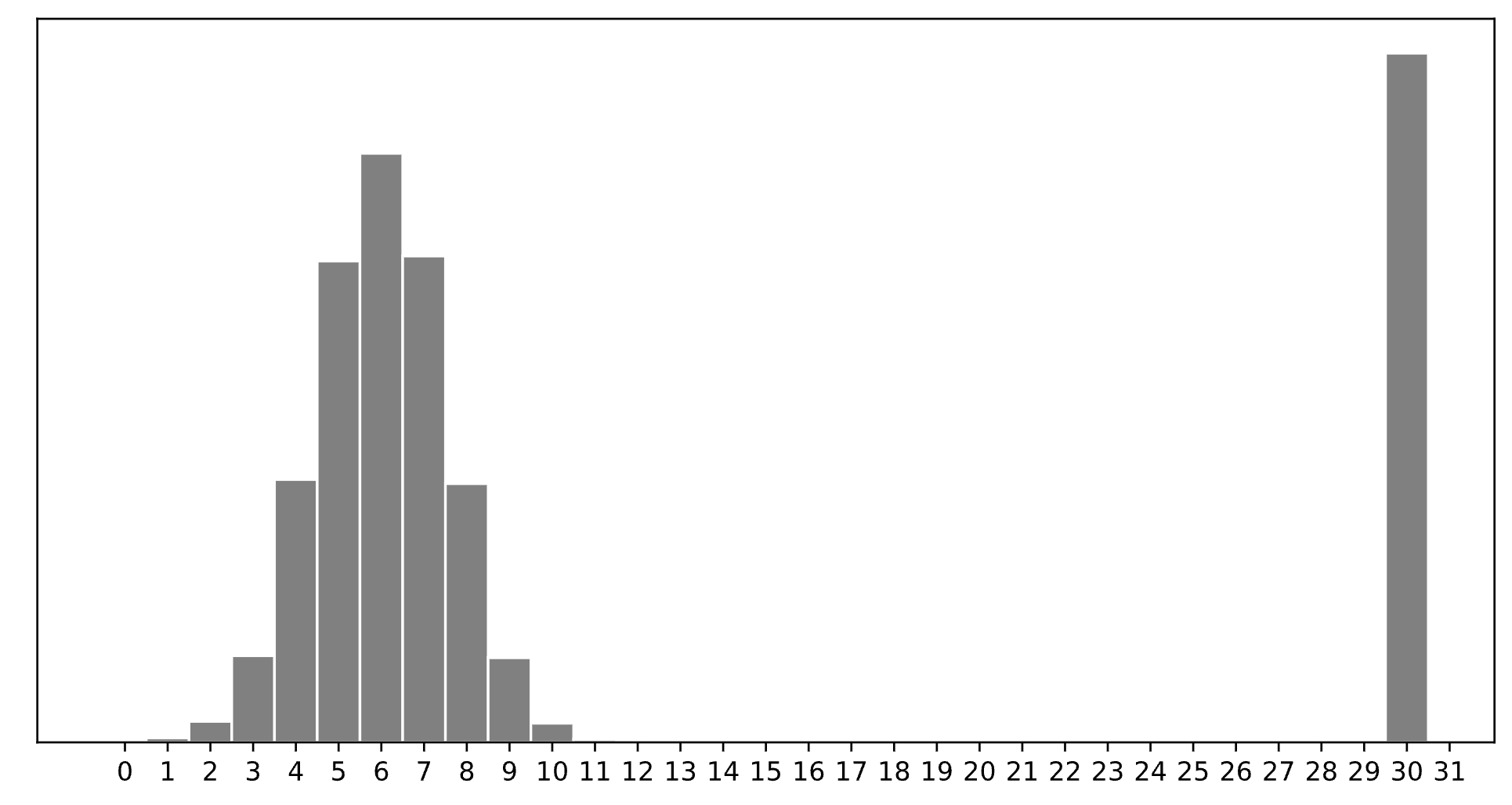
Consider a dataset of n integers, y_1, y_2, ..., y_n, whose histogram is given below:

Which of the following is closest to the constant prediction h^* that minimizes:
\displaystyle \frac{1}{n} \sum_{i = 1}^n \begin{cases} 0 & y_i = h \\ 1 & y_i \neq h \end{cases}
1
5
6
7
11
15
30
30.
The minimizer of empirical risk for the constant model when using zero-one loss is the mode.
Which of the following is closest to the constant prediction h^* that minimizes: \displaystyle \frac{1}{n} \sum_{i = 1}^n |y_i - h|
1
5
6
7
11
15
30
7.
The minimizer of empirical risk for the constant model when using absolute loss is the median. If the bar at 30 wasn’t there, the median would be 6, but the existence of that bar drags the “halfway” point up slightly, to 7.
Which of the following is closest to the constant prediction h^* that minimizes: \displaystyle \frac{1}{n} \sum_{i = 1}^n (y_i - h)^2
1
5
6
7
11
15
30
11.
The minimizer of empirical risk for the constant model when using squared loss is the mean. The mean is heavily influenced by the presence of outliers, of which there are many at 30, dragging the mean up to 11. While you can’t calculate the mean here, given the large right tail, this question can be answered by understanding that the mean must be larger than the median, which is 7, and 11 is the next biggest option.
Which of the following is closest to the constant prediction h^* that minimizes: \displaystyle \lim_{p \rightarrow \infty} \frac{1}{n} \sum_{i = 1}^n |y_i - h|^p
1
5
6
7
11
15
30
15.
The minimizer of empirical risk for the constant model when using infinity loss is the midrange, i.e. halfway between the min and max.
Source: Spring 2024 Final, Problem 2
Consider a dataset of 3 values, y_1 < y_2 < y_3, with a mean of 2. Let Y_\text{abs}(h) = \frac{1}{3} \sum_{i = 1}^3 |y_i - h| represent the mean absolute error of a constant prediction h on this dataset of 3 values.
Similarly, consider another dataset of 5 values, z_1 < z_2 < z_3 < z_4 < z_5, with a mean of 12. Let Z_\text{abs}(h) = \frac{1}{5} \sum_{i = 1}^5 |z_i - h| represent the mean absolute error of a constant prediction h on this dataset of 5 values.
Suppose that y_3 < z_1, and that T_\text{abs}(h) represents the mean absolute error of a constant prediction h on the combined dataset of 8 values, y_1, ..., y_3, z_1, ..., z_5.
Fill in the blanks:
“{ i } minimizes Y_\text{abs}(h), { ii } minimizes Z_\text{abs}(h), and { iii } minimizes T_\text{abs}(h).”
y_1
any value between y_1 and y_2 (inclusive)
y_2
y_3
z_1
z_1
z_2
any value between z_2 and z_3 (inclusive)
any value between z_2 and z_4 (inclusive)
z_3
y_2
y_3
any value between y_3 and z_1 (inclusive)
any value between z_1 and z_2 (inclusive)
any value between z_2 and z_3 (inclusive)
The values of the three blanks are: y_2, z_3, and any value between z_1 and z_2 (inclusive).
For the first blank, we know the median of the y-dataset minimizes mean absolute error of a constant prediction on the y-dataset. Since y_1 < y_2 < y_3, y_2 is the unique minimizer.
For the second blank, we can also use the fact that the median of the z-dataset minimizes mean absolute error of a constant prediction on the z-dataset. Since z_1 < z_2 < z_3 < z_4 < z_5, z_3 is the unique minimizer.
For the third blank, we know that when there are an odd number of data points in a dataset, any values between the middle two (inclusive) minimize mean absolute error. Here, the middle two in the full dataset of 8 are z_1 and z_2.
For any h, it is true that:
T_\text{abs}(h) = \alpha Y_\text{abs}(h) + \beta Z_\text{abs}(h)
for some constants \alpha and \beta. What are the values of \alpha and \beta? Give your answers as integers or simplified fractions with no variables.
\alpha = \frac{3}{8}, \beta = \frac{5}{8}.
To find \alpha and \beta, we need to construct a similar-looking equation to the one above. We can start by looking at our equation for T_\text{abs}(h):
T_\text{abs}(h) = \frac{1}{8} \sum_{i = 1}^8 |t_i - h|
Now, we can split the sum on the right hand side into two sums, one for our y data points and one for our z data points:
T_\text{abs}(h) = \frac{1}{8} \left(\sum_{i = 1}^3 |y_i - h| + \sum_{i = 1}^5 |z_i - h|\right)
Each of these two mini sums can be represented in terms of Y_\text{abs}(h) and Z_\text{abs}(h):
T_\text{abs}(h) = \frac{1}{8} \left(3 \cdot Y_\text{abs}(h) + 5 \cdot Z_\text{abs}(h)\right) T_\text{abs}(h) = \frac38 \cdot Y_\text{abs}(h) + \frac58 \cdot Z_\text{abs}(h)
By looking at this final equation we’ve built, it is clear that \alpha = \frac{3}{8} and \beta = \frac{5}{8}.
Show that Y_\text{abs}(z_1) = z_1 - 2.
Hint: Use the fact that you know the mean of y_1, y_2, y_3.
We can start by plugging z_1 into Y_\text{abs}(h):
Y_\text{abs}(z_1) = \frac{1}{3} \left( | z - y_1 | + | z - y_2 | + |z - y_3| \right)
Since z_1 > y_3 > y_2 > y_1, all of the absolute values can be dropped and we can write:
Y_\text{abs}(z_1) = \frac{1}{3} \left( (z_1 - y_1) + (z_1 - y_2) + (z_3 - y_3) \right)
This can be simplified to:
Y_\text{abs}(h) = \frac{1}{3} \left( 3z_1 - (y_1 + y_2 + y_3) \right) = \frac{1}{3} \left( 3z_1 - 3 \cdot \bar{y}\right) = z_1 - \bar{y} = z_1 - 2.
Suppose the mean absolute deviation from the median in the full dataset of 8 values is 6. What is the value of z_1?
Hint: You’ll need to use the results from earlier parts of this question.
2
3
5
6
7
9
11
3.
We are given that T_\text{abs}(\text{median}) = 6. This means that any value (inclusive) between z_1 and z_2 minimize T_\text{abs}(h), with the output being always being 6. So, T_\text{abs}(z_1) = 6. Let’s see what happens when we plug this into T_\text{abs}(h) = \frac{3}{8} Y_\text{abs}(h) + \frac{5}{8} Z_\text{abs}(h) from earlier:
T_\text{abs}(z_1) = \frac{3}{8} Y_\text{abs}(z_1) + \frac{5}{8} Z_\text{abs}(z_1) (6) = \frac{3}{8} Y_\text{abs}(z_1) + \frac{5}{8} Z_\text{abs}(z_1)
If we could write Y_\text{abs}(z_1) and Z_\text{abs}(z_1) in terms of z_1, we could solve for z_1 and our work would be done, so let’s do that. Y_\text{abs}(z_1) = z_1 - 2 from earlier. Z_\text{abs}(z_1) simplifies as follows (knowing that \bar{z} = 12):
Z_\text{abs}(z_1) = \frac{1}{5} \sum_{i = 1}^5 |z_i - z_1| Z_\text{abs}(z_1) = \frac{1}{5} \left(|z_1 - z_1| + |z_2 - z_1| + |z_3 - z_1| + |z_4 - z_1| + |z_5 - z_1|\right) Z_\text{abs}(z_1) = \frac{1}{5} \left(0 + (z_2 + z_3 + z_4 + z_5) - 4z_1\right) Z_\text{abs}(z_1) = \frac{1}{5} \left((z_2 + z_3 + z_4 + z_5) - 4z_1 + (z_1 - z_1)\right) Z_\text{abs}(z_1) = \frac{1}{5} \left((z_1 + z_2 + z_3 + z_4 + z_5) - 5z_1\right) Z_\text{abs}(z_1) = \bar{z} - z_1 Z_\text{abs}(z_1) = (12) - z_1
Subbing back into our main equation:
(6) = \frac{3}{8} Y_\text{abs}(z_1) + \frac{5}{8} Z_\text{abs}(z_1) 6 = \frac{3}{8}(z_1 - 2) + \frac{5}{8}(12 - z_1) z_1 = 3